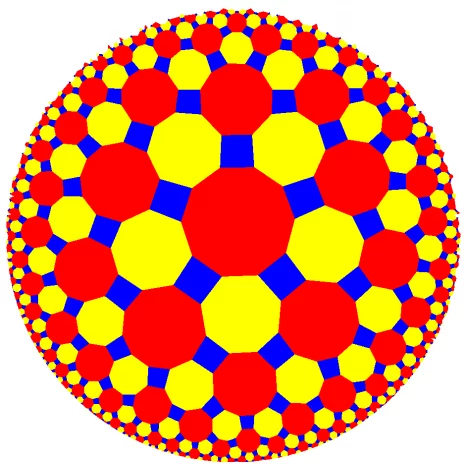
Snub trihexagonal tiling
In geometry, the snub hexagonal tiling (or snub trihexagonal tiling) is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex. It has Schläfli symbol of sr{3,6}. The snub tetrahexagonal tiling is a related hyperbolic tiling with Schläfli symbol sr{4,6}.
Conway calls it a snub hextille, constructed as a snub operation applied to a hexagonal tiling (hextille).
There are 3 regular and 8 semiregular tilings in the plane. This is the only one which does not have a reflection as a symmetry.
There is only one uniform coloring of a snub trihexagonal tiling. (Naming the colors by indices (3.3.3.3.6): 11213.)
Circle packing
The snub trihexagonal tiling can be used as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 5 other circles in the packing (kissing number). The lattice domain (red rhombus) repeats 6 distinct circles. The hexagonal gaps can be filled by exactly one circle, leading to the densest packing from the triangular tiling#circle packing.
...
wikipedia.org 2
0
0

Elongated triangular tiling
In geometry, the elongated triangular tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. It is named as a triangular tiling elongated by rows of squares, and given Schläfli symbol {3,6}:e.
Conway calls it a isosnub quadrille.
There are 3 regular and 8 semiregular tilings in the plane. This tiling is similar to the snub square tiling which also has 3 triangles and two squares on a vertex, but in a different order.
Construction
It is also the only uniform tiling that can't be created as a Wythoff construction. It can be constructed as alternate layers of apeirogonal prisms and apeirogonal antiprisms.
Uniform colorings
There is one uniform colorings of an elongated triangular tiling. Two 2-uniform colorings have a single vertex figure, 11123, with two colors of squares, but are not 1-uniform, repeated either by reflection or glide reflection, or in general each row of squares can be shifted around independently. The 2-uniform tilings are also called Archimedean colorings. There are...
wikipedia.org 1
0
0
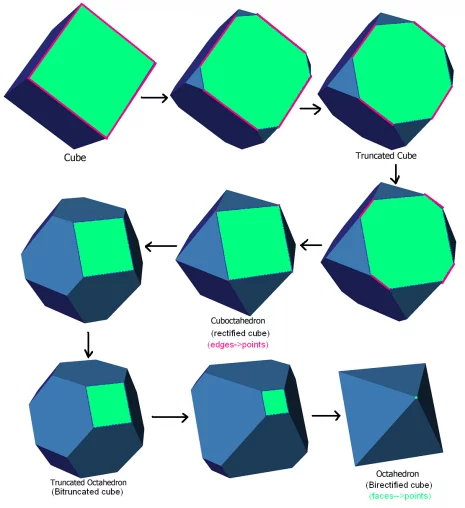
Bitruncation
In geometry, a bitruncation is an operation on regular polytopes. It represents a truncation beyond rectification. The original edges are lost completely and the original faces remain as smaller copies of themselves.
Bitruncated regular polytopes can be represented by an extended Schläfli symbol notation t1,2{p,q,...} or 2t{p,q,...}.
In regular polyhedra and tilings
For regular polyhedra, a bitruncated form is the truncated dual. For example, a bitruncated cube is a truncated octahedron.
In regular 4-polytopes and honeycombs
For regular 4-polytope, a bitruncated form is a dual-symmetric operator. A bitruncated 4-polytope is the same as the bitruncated dual.
A regular polytope (or honeycomb) {p, q, r} will have its {p, q} cells bitruncated into truncated {q, p} cells, and the vertices are replaced by truncated {q, r} cells.
wikipedia.org 0
0
0

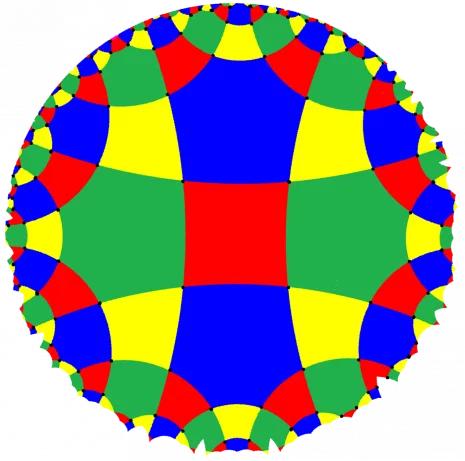
Omnitruncated polyhedron
In geometry, an omnitruncated polyhedron is a truncated quasiregular polyhedron. When they are alternated, they produce the snub polyhedra.
All omnitruncated polyhedra are zonohedra. They have Wythoff symbol p q r | and vertex figures as 2p.2q.2r.
More generally an omnitruncated polyhedron is a bevel operator in Conway polyhedron notation.
List of convex omnitruncated polyhedra
There are three convex forms. They can be seen as red faces of one regular polyhedron, yellow or green faces of the dual polyhedron, and blue faces at the truncated vertices of the quasiregular polyhedron.
List of nonconvex omnitruncated polyhedra
There are 5 nonconvex uniform omnitruncated polyhedra.
Other even-sided nonconvex polyhedra
There are 7 nonconvex forms with mixed Wythoff symbols p q (r s) |, and bow-tie shaped vertex figures, 2p.2q.-2q.-2p. They are not true omnitruncated polyhedra: the true omnitruncates have coinciding...
wikipedia.org 0
0
0

Pentagonal tiling
In geometry, a pentagonal tiling is a tiling of the plane where each individual piece is in the shape of a pentagon.
A regular pentagonal tiling on the Euclidean plane is impossible because the internal angle of a regular pentagon, 108°, is not a divisor of 360°, the angle measure of a whole turn. However, they can tile the hyperbolic plane and the sphere.
Monohedral convex pentagonal tilings
Fifteen types of convex pentagons are known to tile the plane monohedrally (i.e. with one type of tile). The most recent one was discovered in 2015. This list has been shown to be complete by Rao (2017). Bagina (2011) showed that there are only eight edge-to-edge convex types, a result obtained independently by Sugimoto (2012).
Michaël Rao of the École normale supérieure de Lyon claimed on 1 May 2017 to have found the proof that there are in fact no more than these 15 monohedral convex pentagonal tilings
Each enumerated tiling family contains pentagons that belong to no other type; however, some individual pentagons may belong to multiple types. In addition, some of the pentagons...
wikipedia.org 0
0
0
Uniform tilings in hyperbolic plane
In hyperbolic geometry, a uniform (regular, quasiregular or semiregular) hyperbolic tiling is an edge-to-edge filling of the hyperbolic plane which has regular polygons as faces and is vertex-transitive (transitive on its vertices, isogonal, i.e. there is an isometry mapping any vertex onto any other). It follows that all vertices are congruent, and the tiling has a high degree of rotational and translational symmetry.
Uniform tilings can be identified by their vertex configuration, a sequence of numbers representing the number of sides of the polygons around each vertex. For example 7.7.7 represents the heptagonal tiling which has 3 heptagons around each vertex. It is also regular since all the polygons are the same size, so it can also be given the Schläfli symbol {7,3}.
Uniform tilings may be regular (if also face- and edge-transitive), quasi-regular (if edge-transitive but not face-transitive) or semi-regular (if neither edge- nor face-transitive). For right triangles (p q 2), there are two regular tilings, represented by Schläfli symbol {p,q} and {q,p}.
wikipedia.org 0
0
0

https://upload.wikimedia.org/wikipedia/en/5/55/Escher_Circle_Limit_III.jpg
wikimedia.org 0
0
0

Rhombitrioctagonal tiling
In geometry, the rhombitrioctagonal tiling is a semiregular tiling of the hyperbolic plane. At each vertex of the tiling there is one triangle and one octagon, alternating between two squares. The tiling has Schläfli symbol rr{8,3}. It can be seen as constructed as a rectified trioctagonal tiling, r{8,3}, as well as an expanded octagonal tiling or expanded order-8 triangular tiling.
Symmetry
This tiling has [8,3], (*832) symmetry. There is only one uniform coloring.
Similar to the Euclidean rhombitrihexagonal tiling, by edge-coloring there is a half symmetry form (3*4) orbifold notation. The octagons can be considered as truncated squares, t{4} with two types of edges. It has Coxeter diagram , Schläfli symbol s2{3,8}. The squares can be distorted into isosceles trapezoids. In the limit, where the rectangles degenerate into edges, an order-8 triangular tiling results, constructed as an snub tritetratrigonal tiling, .
Related polyhedra and tilings
From a Wythoff construction there are ten hyperbolic uniform tilings...
wikipedia.org 0
0
0
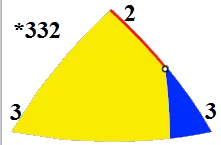
Cantic octagonal tiling
In geometry, the tritetratrigonal tiling or shieldotritetragonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t1,2(4,3,3). It can also be named as a cantic octagonal tiling, h2{8,3}.
Dual tiling
Related polyhedra and tiling
References
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
"Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
wikipedia.org 0
0
0

Truncated order-7 heptagonal tiling
In geometry, the truncated order-7 heptagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of t0,1{7,7}, constructed from one heptagons and two tetrakaidecagons around every vertex.
Related tilings
See also
Square tiling
Uniform tilings in hyperbolic plane
List of regular polytopes
References
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
"Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
wikipedia.org 1
0
0

Triangular tiling
In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.
Conway calls it a deltille, named from the triangular shape of the Greek letter delta (Δ). The triangular tiling can also be called a kishextille by a kis operation that adds a center point and triangles to replace the faces of a hextille.
It is one of three regular tilings of the plane. The other two are the square tiling and the hexagonal tiling.
Uniform colorings
There are 9 distinct uniform colorings of a triangular tiling. (Naming the colors by indices on the 6 triangles around a vertex: 111111, 111112, 111212, 111213, 111222, 112122, 121212, 121213, 121314) Three of them can be derived from others by repeating colors: 111212 and 111112 from 121213 by combining 1 and 3, while 111213 is reduced from 121314.
There is one class of Archimedean colorings, 111112, (marked with...
wikipedia.org 0
0
0

4-5 kisrhombille
In geometry, the 4-5 kisrhombille or order-4 bisected pentagonal tiling is a semiregular dual tiling of the hyperbolic plane. It is constructed by congruent right triangles with 4, 8, and 10 triangles meeting at each vertex.
The name 4-5 kisrhombille is by Conway, seeing it as a 4-5 rhombic tiling, divided by a kis operator, adding a center point to each rhombus, and dividing into four triangles.
The image shows a Poincaré disk model projection of the hyperbolic plane.
It is labeled V4.8.10 because each right triangle face has three types of vertices: one with 4 triangles, one with 8 triangles, and one with 10 triangles.
Dual tiling
It is the dual tessellation of the truncated tetrapentagonal tiling which has one square and one octagon and one decagon at each vertex.
References
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
See also
Hexakis triangular tiling...
wikipedia.org 0
0
0

Heptagonal tiling
In geometry, the heptagonal tiling is a regular tiling of the hyperbolic plane. It is represented by Schläfli symbol of {7,3}, having three regular heptagons around each vertex.
Images
Related polyhedra and tilings
This tiling is topologically related as a part of sequence of regular polyhedra with Schläfli symbol {n,3}.
From a Wythoff construction there are eight hyperbolic uniform tilings that can be based from the regular heptagonal tiling.
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms.
Hurwitz surfaces
The symmetry group of the tiling is the (2,3,7) triangle group, and a fundamental domain for this action is the (2,3,7) Schwarz triangle. This is the smallest hyperbolic Schwarz triangle, and thus, by the proof of Hurwitz's automorphisms theorem, the tiling is the universal tiling that covers all Hurwitz surfaces (the Riemann surfaces with maximal symmetry group), giving them a tiling by heptagons...
wikipedia.org 0
0
0
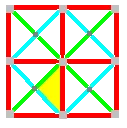
Tetrakis square tiling
In geometry, the tetrakis square tiling is a tiling of the Euclidean plane. It is a square tiling with each square divided into four isosceles right triangles from the center point, forming an infinite arrangement of lines. It can also be formed by subdividing each square of a grid into two triangles by a diagonal, with the diagonals alternating in direction, or by overlaying two square grids, one rotated by 45 degrees from the other and scaled by a factor of √2.
Conway calls it a kisquadrille, represented by a kis operation that adds a center point and triangles to replace the faces of a square tiling (quadrille). It is also called the Union Jack lattice because of the resemblance to the UK flag of the triangles surrounding its degree-8 vertices.
It is labeled V4.8.8 because each isosceles triangle face has two types of vertices: one with 4 triangles, and two with 8 triangles.
Dual tiling
It is the dual tessellation of the truncated square tiling which has one square and two octagons at each vertex.
Applications
A 5 ...
wikipedia.org 1
0
0

Octagonal tiling
In geometry, the octagonal tiling is a regular tiling of the hyperbolic plane. It is represented by Schläfli symbol of {8,3}, having three regular octagons around each vertex.
Uniform colorings
Like the hexagonal tiling of the Euclidean plane, there are 3 uniform colorings of this hyperbolic tiling. The dual tiling V8.8.8 represents the fundamental domains of [(4,4,4)] symmetry.
Related polyhedra and tilings
This tiling is topologically part of sequence of regular polyhedra and tilings with Schläfli symbol {n,3}.
And also is topologically part of sequence of regular tilings with Schläfli symbol {8,n}.
From a Wythoff construction there are ten hyperbolic uniform tilings that can be based from the regular octagonal tiling.
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 10 forms.
See also
Tilings of regular polygons
List of uniform planar tilings
List of regular polytopes...
wikipedia.org 2
0
0

Snub trihexagonal tiling
In geometry, the snub hexagonal tiling (or snub trihexagonal tiling) is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex. It has Schläfli symbol of sr{3,6}. The snub tetrahexagonal tiling is a related hyperbolic tiling with Schläfli symbol sr{4,6}.
Conway calls it a snub hextille, constructed as a snub operation applied to a hexagonal tiling (hextille).
There are 3 regular and 8 semiregular tilings in the plane. This is the only one which does not have a reflection as a symmetry.
There is only one uniform coloring of a snub trihexagonal tiling. (Naming the colors by indices (3.3.3.3.6): 11213.)
Circle packing
The snub trihexagonal tiling can be used as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 5 other circles in the packing (kissing number). The lattice domain (red rhombus) repeats 6 distinct circles. The hexagonal gaps can be filled by exactly one circle, leading to the densest packing from the triangular tiling#circle packing.
...
wikipedia.org 0
0
0

Circle Limit III
Circle Limit III is a woodcut made in 1959 by Dutch artist M. C. Escher, in which "strings of fish shoot up like rockets from infinitely far away" and then "fall back again whence they came".
It is one of a series of four woodcuts by Escher depicting ideas from hyperbolic geometry. Dutch physicist and mathematician Bruno Ernst called it "the best of the four".
Inspiration
Escher became interested in tesselations of the plane after a 1936 visit to the Alhambra in Granada, Spain, and from the time of his 1937 artwork Metamorphosis I he had begun incorporating tessellated human and animal figures into his artworks.
In a 1958 letter from Escher to H. S. M. Coxeter, Escher wrote that he was inspired to make his Circle Limit series by a figure in Coxeter's article "Crystal Symmetry and its Generalizations". Coxeter's figure depicts a tessellation of the hyperbolic plane by right triangles with angles of 30°, 45°, and 90°; triangles with these angles are possible in hyperbolic geometry but not in Euclidean geometry. This tessellation may be interpreted as depicting the lines of reflection...
wikipedia.org 1
0
0

Infinite-order pentagonal tiling
In 2-dimensional hyperbolic geometry, the infinite-order pentagonal tiling is a regular tiling. It has Schläfli symbol of {5,∞}. All vertices are ideal, located at "infinity", seen on the boundary of the Poincaré hyperbolic disk projection.
Symmetry
There is a half symmetry form, , seen with alternating colors:
Related polyhedra and tiling
This tiling is topologically related as a part of sequence of regular polyhedra and tilings with vertex figure (5n).
See also
Square tiling
Uniform tilings in hyperbolic plane
List of regular polytopes
References
John H. Conway; Heidi Burgiel; Chaim Goodman-Strass (2008). "Chapter 19, The Hyperbolic Archimedean Tessellations". The Symmetries of Things. ISBN 978-1-56881-220-5.
wikipedia.org 0
0
0

Cairo pentagonal tiling
In geometry, the Cairo pentagonal tiling is a dual semiregular tiling of the Euclidean plane. It is given its name because several streets in Cairo are paved in this design. It is one of 15 known monohedral pentagon tilings.
It is also called MacMahon's net after Percy Alexander MacMahon and his 1921 publication New Mathematical Pastimes.
Conway calls it a 4-fold pentille.
As a 2-dimensional crystal net, it shares a special feature with the honeycomb net. Both nets are examples of standard realization, the notion introduced by M. Kotani and T. Sunada for general crystal nets.
Geometry
These are not regular pentagons: their sides are not equal (they have four long ones and one short one in the ratio 1:sqrt(3)-1), and their angles in sequence are 120°, 120°, 90°, 120°, 90°. It is represented by with face configuration V3.3.4.3.4.
It is similar to the prismatic pentagonal tiling with face configuration V3.3.3.4.4, which has its right angles adjacent to each other.
Variations
The Cairo pentagonal tiling has two lower...
wikipedia.org 1
0
0

Rhombille tiling
In geometry, the rhombille tiling, also known as tumbling blocks, reversible cubes, or the dice lattice, is a tessellation of identical 60° rhombi on the Euclidean plane. Each rhombus has two 60° and two 120° angles; rhombi with this shape are sometimes also called diamonds. Sets of three rhombi meet at their 120° angles and sets of six rhombi meet at their 60° angles.
Properties
The rhombille tiling can be seen as a subdivision of a hexagonal tiling with each hexagon divided into three rhombi meeting at the center point of the hexagon. This subdivision represents a regular compound tiling. It can also be seen as a subdivision of four hexagonal tilings with each hexagon divided into 12 rhombi.
The diagonals of each rhomb are in the ratio 1:√3. This is the dual tiling of the trihexagonal tiling or kagome lattice. As the dual to a uniform tiling, it is one of eleven possible Laves tilings, and in the face configuration for monohedral tilings it is denoted [3.6.3.6].
It is also one of 56 possible isohedral tilings by quadrilaterals, and one of only eight tilings of the plane in...
wikipedia.org 0
0
0

Cairo pentagonal tiling
In geometry, the Cairo pentagonal tiling is a dual semiregular tiling of the Euclidean plane. It is given its name because several streets in Cairo are paved in this design. It is one of 15 known monohedral pentagon tilings.
It is also called MacMahon's net after Percy Alexander MacMahon and his 1921 publication New Mathematical Pastimes.
Conway calls it a 4-fold pentille.
As a 2-dimensional crystal net, it shares a special feature with the honeycomb net. Both nets are examples of standard realization, the notion introduced by M. Kotani and T. Sunada for general crystal nets.
Geometry
These are not regular pentagons: their sides are not equal (they have four long ones and one short one in the ratio 1:sqrt(3)-1), and their angles in sequence are 120°, 120°, 90°, 120°, 90°. It is represented by with face configuration V3.3.4.3.4.
It is similar to the prismatic pentagonal tiling with face configuration V3.3.3.4.4, which has its right angles adjacent to each other.
Variations
The Cairo pentagonal tiling has two lower...
wikipedia.org 0
0
0